מהי משוואה ריבועית?
משוואה ריבועית היא משוואה ממעלה שניה, כלומר בעלת הצורה
\(ax^{2}+bx+c=0\)
המשוואה הזאת מתארת פרבולה, לעומת משוואה ממעלה ראשונה שמתארת למעשה קו ישר
\(ax+b=0\)
משוואה ריבועית ניתן לפתור בכמה צורות, אחת מהן היא פירוק המשוואה בצורת פירוק הטרינום (יש לנו כאן מחשבון של פירוק טרינום).
מה בעצם מקבלים בפתרונות המשוואה?
אם מכניסים את המשוואה הריבועית על מערכת צירים לפי
\(y=ax^{2}+bx+c\)פתרונות המשוואה יסמנו את נקודות החיתוך של המשוואה עם ציר ה x כלומר מה יהיה ערכו של x כאשר y=0/
משוואה ריבועית ללא פתרונות
למשל \(y=x^2-2x+2\) היא משוואה ללא פתרונות, כלומר אינה חותכת את ציר הx בשום מקום, היא נמצאת כולה מעל לציר הx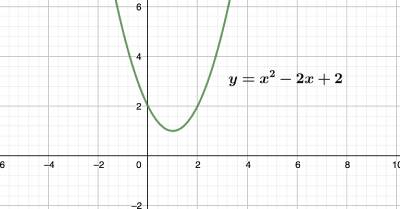
משוואה ריבועית עם פתרון יחיד
למשל \(y=ֿ\frac{1}{2}x^2\) היא משוואה אם פתרון יחדי, המשוואה ״נוגעת״ בציר הx בנקודה אחת בלבד
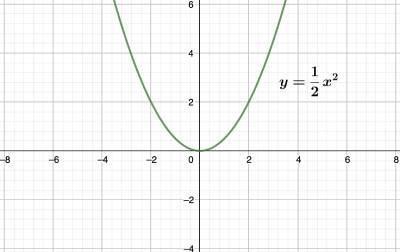
משוואה ריבועית עם שני פתרונות
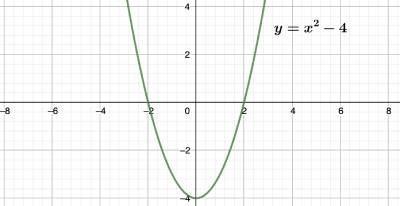
למשל \(y=ֿx^2-4\) היא משוואה עם שני פתרונות, היא חותכת את ציר הx בשני מקומות (הקודקוד שלה נמצא מתחת לציר הx)
למה אנחנו צריכים נוסחה כדי לפתור משוואה ריבועית?
בשונה מפתרון משוואה קווית כמו 2x+3=5 במשוואה ממעלה שניה עולה פתאום משתנה חדש, הריבוע, במקרים בהם למשוואה הריבועית רק פתרון יחיד או שני פתרונות שאחד מהם הוא אפס, הפתרון מסובך יותר, לעיתים אפשר להתמודד עם הפתרון בעזרת שיטת פירוק הטרינום, אך ביתר המקרים נצטרך כלי ״חזק״ שיוכל לתת פתרון לכל סוגי המשוואות הריבועיות, על שלל הפתרונות שלהם, כאן נכנסת למשחק נוסחת השורשים המדוברת
מהי נוסחת השורשים?
כך נראית משוואה ריבועית כללית:
\(ax^2+bx+c=0\)
הם מקדמי המשוואה הריבועית ואותם אנחנו נציב בנוסחת השורשים a,b ו c
נוסחת השורשים נראית כך
\( x_{1,2}=\frac{-b \pm \sqrt{b^{2}-4ac}}{2a} \)
פתרונות המשוואה x1 ו x2 הם
| \( x_{1}=\frac{-b + \sqrt{b^{2}-4ac}}{2a} \) | \( x_{2}=\frac{-b – \sqrt{b^{2}-4ac}}{2a} \) |
את ההצבה שבתוך השורש בנוסחה מכנים דלתא ומסמנים אותה באות Δ
\(\Delta = {b^2-4ac} \)
ניתן לזהות במהירות בעזרת Δ כמה פתרונות יש למשוואה הריבועית
- Δ < 0 למשוואה אין פתרונות בכלל (אם אפשר להוציא שורש ממספר שלילי)
- Δ = 0 למשוואה פתרון יחיד (אפשר גם לומר שלמשוואה שני פתרונות שווים)
- Δ > 0 למשוואה שני פתרונות שונים
זיהוי מקדמי המשוואה הריבועית
כדי לשתמש בנוסחת השורשים בצורה מהירה ולהגיע לשליטה מוחלטת, נצטרך לדעת למצוא את מקדמי המשוואה a,b,c , בואו נעבור על כמה דוגמאות
מצאו את מקדמי המשוואה \(2x^2-3=0\)
כדי למצוא את מקדמי המשוואה, נראה אותו בצורתה המלאה
\(ax^2+bx+c=0\)
למעשה במקרה הזה אנחנו יכולים כתוב את המשוואה גם כך
\(2x^2+0x-3=0\)
ולכן מקדמי המשוואה הם
\(a=2 , b=0 , c=-3\)
מצאו את מקדמי המשוואה \(-x^2+4x=0\)
כדי למצוא את מקדמי המשוואה, נראה אותו בצורתה המלאה
\(ax^2+bx+c=0\)
כמו במקרה הקודם אנחנו יכולים כתוב את המשוואה גם כך
\(-x^2+4x=0\)
ולכן מקדמי המשוואה הם
\(a=-1 , b=4 , c=0\)
מצאו את מקדמי המשוואה \(-x^2-3x+11=0\)
הפעם אנחנו רואים שכל מקדמי המשוואה שונים מאפס ולכן ברור יותר איך לחלץ אותם
\(a=-1 , b=-3 , c=11\)
דוגמאות לשימוש בנוסחת השורשים:
הנה כמה דוגמאות למציאת שורשים המשוואה הריבועית בעזרת השימוש בנוסחת השורשים. בכל תרגיל לא משנה איזה, נעבור על השלבים הבאים:
- נביט במשוואה ונמצא את ערכי המקדמים a,b,c
- נחשב את ערכו של ה-Δ כדי שנוכל להבין כמה פתרונות יש למשוואה
- נציב את המקדמים בנוסחת השורשים ונפתור את המשוואה
- ככה זה פשוט
מצאו את שורשי המשוואה
\(4x^2-16=0\)
תוך כדי שימוש בנוסחאת השורשיםפתרון:
ראשית נראה שמקדמי המשוואה הריבועית הם
\(a=4 , b=0 , c=-16\)נבדוק את ה Δ של המשוואה
\(\Delta = {b^2-4ac} = 0^2 – 4 \cdot 4 \cdot (-16)\)\(\Delta = 0 + 256 = 256\)נמצא את שורשי המשוואה ע״י הצבת המקדמים בנוסחת השורשים
\( x_{1,2}=\frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\)
ונקבל
\( x_{1}=\frac{0 + \sqrt{0^{ 2}-4\cdot 4\cdot 16}}{2 \cdot 4} \)
\( x_{1}=\frac{+ \sqrt{256}}{8} = \frac{16}{8} = 2\)
\( x_{2}=\frac{0 – \sqrt{0^{2}-4\cdot 4 \cdot 16}}{2\cdot 4}\)
\( x_{2}=\frac{- \sqrt{256}}{8} = -\frac{16}{8} = -2\)
מצאו את שורשי המשוואה
\(4x^2+14x-8=0\)
תוך כדי שימוש בנוסחאת השורשיםפתרון:
ראשית נראה שמקדמי המשוואה הריבועית הם
\(a=4 , b=14 , c=-8\)נבדוק את ערכה של הΔ (מה שיש מתחת לשורש)
\(\Delta = {b^2-4ac} = 14^2 – 4 \cdot 4 \cdot (-8)\)\(\Delta = 196 + 128 = 324\)כעת נפתור את המשוואה ע״י הצבת המקדמים בנוסחת השורשים
\( x_{1,2}=\frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\)
\( x_{1}=\frac{-4+ \sqrt{324}}{8} = \frac{-4+18}{8} = \frac{1}{2}\)
\( x_{2}=\frac{-4- \sqrt{324}}{8} = -\frac{-4+18}{8} = -4\)
מצאו את שורשי המשוואה
\(2x^2+3x+4=0\)
תוך כדי שימוש בנוסחאת השורשיםפתרון:
ראשית נראה שמקדמי המשוואה הריבועית הם
\(a=2 , b=3 , c=4\)נבדוק את ערכה של ה-Δ (מה שיש מתחת לשורש)
\(\Delta = {b^2-4ac} = 3^2 – 4 \cdot 2 \cdot 4 \)\(\Delta = 9 – 32 = -23\)מכיוון שערך ה-Δ שלילי, אין למשוואה פתרונות
באופן כללי אפשר לומר שכאשר ה-Δ שלילית וערכו של a חיובי כל הפרבולה נמצאת מעל ציר ה x ולא חותכת אותו לעולם
מחשבון לפתירת משוואה ריבועית
הכנו עבורכם את המחשבון הכי מתקדם לפתרון משוואה ריבועית שתמצאו ברשת, הכניסו את המקדמים של המשוואה הריבועית a,b,c וקבלו פתרון למשוואה כולל הסבר ודרך מלאים. שתפו
